0. A Technical Review of Early Applications of Quantum Computing in Molecular Simulation

1. Introduction

The accurate simulation of molecular and material properties is fundamental to advancements across numerous scientific and industrial domains, including drug discovery, catalyst design, and the development of novel materials for energy and technology applications . Historically, classical computing methods have been indispensable in these pursuits. However, they face inherent and significant limitations when confronting the complex quantum mechanical nature of many-electron systems .

A primary challenge for classical computers lies in accurately modeling complex electronic structures, particularly the intricate electron-electron correlation effects . Classical approaches often rely on approximations, such as assuming an "averaged relationship" between electrons, which can lead to a significant loss of accuracy, especially for systems with a large number of electrons or for strongly correlated systems where particles exhibit high entanglement or superposition . For instance, simulating molecular behavior—such as protein folding or drug-target binding—requires solving the Schrödinger equation, which quickly becomes intractable on classical systems due to the exponential growth of variables and configurations involved . This exponential complexity limits the scale and accuracy of simulations, rendering many crucial problems computationally prohibitive and restricting the utility of classical simulations for practical applications . For example, accurately predicting therapeutic compound efficacy or identifying novel drug candidates requires simulating molecular interactions at an unprecedented scale, a task beyond the current capabilities of classical systems .

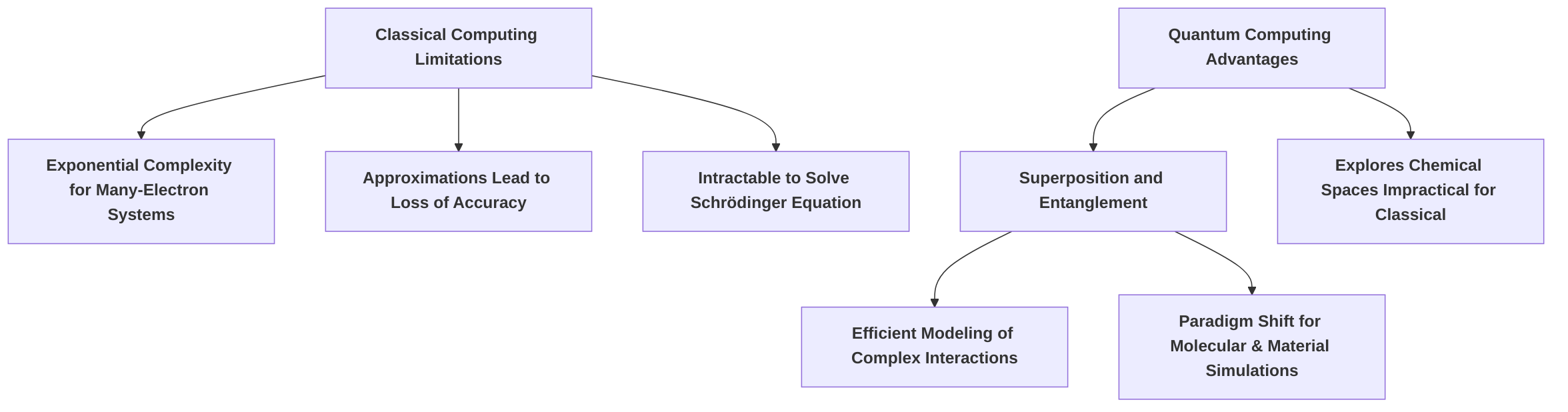
Quantum computing offers a transformative approach to overcome these limitations by leveraging the fundamental principles of quantum mechanics, such as superposition and entanglement . Unlike classical bits that are restricted to states of 0 or 1, quantum bits (qubits) can exist in multiple states simultaneously, allowing for more efficient modeling of complex interactions inherent to molecular and material systems . This capability represents a paradigm shift for computational challenges in drug discovery and materials science, enabling researchers to explore chemical spaces and simulate molecular behaviors that are otherwise impractical to analyze .

The anticipated impact of quantum computing in these fields is profound. In drug discovery, it promises to accelerate the process by enabling more accurate predictions of therapeutic compound efficacy, identifying novel drug candidates, and enhancing personalized medicine development, thereby reducing trial-and-error in lab testing . Collaborations, such as the one between IonQ, AstraZeneca, AWS, and NVIDIA, are already exploring how hybrid quantum-classical computing can speed up simulations of reaction steps to identify viable drug candidates earlier . In materials science, quantum computing can lead to the design of more efficient batteries, cleaner industrial processes, and advanced materials by efficiently simulating electronic structures and atomic core interactions, even for non-cubic structures, using techniques like pseudopotentials . While the field is still in its nascent stages, with many applications showing early promise but requiring improvements across the quantum computing stack, from qubits to quantum error correction , early demonstrations have shown significant advancements. For instance, hybrid quantum-classical methods have been proven capable of accurately simulating complex molecules using current-generation quantum computers, often without requiring fault-tolerant systems . The Variational Quantum Eigensolver (VQE), a flagship algorithm, has been particularly instrumental in simulating ground-state properties for molecular systems on noisy intermediate-scale quantum (NISQ) devices .

This survey aims to provide a comprehensive review of the foundational quantum algorithms and their initial applications in molecular simulation and materials science. It seeks to lay the groundwork for a more detailed discussion in subsequent sections, emphasizing that quantum computing represents a significant evolutionary step over classical methods . By mapping the nascent landscape of quantum computing in these fields, this review highlights its potential to solve complex problems with unprecedented accuracy and speed, ultimately driving advancements in areas ranging from catalyst design to battery materials . The scope encompasses both the theoretical underpinnings and early-stage demonstrations of this transformative technology, focusing on areas where classical methods struggle and quantum computers excel, such as multi-metal systems and heterogeneous catalysis .

2. Foundational Concepts and Quantum Computing Principles for Molecular Simulation

The application of quantum computing to molecular simulation fundamentally rests upon translating intricate molecular electronic structure problems into a quantum mechanical framework amenable to quantum processors . This section elucidates the theoretical underpinnings that enable quantum computers to simulate molecular systems, beginning with the representation of molecular electronic structure problems, followed by a discussion of fundamental quantum phenomena leveraged, an overview of relevant quantum algorithms, and a critical comparison of fermion-to-qubit transformation techniques and the theoretical advantages of leading quantum algorithms.

The initial step involves formulating the molecular electronic structure Hamiltonian in a second-quantized form, utilizing creation ($a^{\dagger}*{p}$) and annihilation ($a*{q}$) operators to describe electron interactions within molecules . This representation inherently incorporates prior knowledge about electron occupation in energy levels, potentially reducing the required qubit count . The challenge then shifts to transforming these fermionic systems into qubit systems, which is essential for algorithms to map the non-local nature of fermionic interactions to local qubit operations, addressing the Pauli exclusion principle inherent to electrons . This transformation is crucial for enabling the representation of complex many-body electron correlations on quantum hardware.

Different fermion-to-qubit transformation techniques, such as Jordan-Wigner, Bravyi-Kitaev, and parity transformations, each have distinct implications for resource overhead, including qubit count and circuit depth . The Jordan-Wigner transformation, while conceptually straightforward, often leads to significant circuit depth due to its non-local operations. In contrast, techniques like Bravyi-Kitaev and parity transformations aim to reduce circuit depth and optimize qubit usage, with the parity transformation directly relating qubit count to the number of spin-orbitals . The selection of an appropriate transformation technique profoundly impacts the feasibility and accuracy of early quantum simulations on current noisy intermediate-scale quantum (NISQ) devices.

Furthermore, quantum computers harness fundamental quantum phenomena such as superposition and entanglement to perform computations, enabling the processing of exponentially larger datasets and parallel computation . These phenomena allow for the efficient simulation of quantum systems like chemical reactions and molecular interactions, which are intractable for classical computers due to the exponential increase in computational requirements with system size .

Among the relevant quantum algorithms, the Variational Quantum Eigensolver (VQE) and Quantum Phase Estimation (QPE) are central to molecular simulation. VQE is a hybrid quantum-classical algorithm particularly suited for NISQ devices, designed to estimate the ground-state energy of molecular systems by iteratively optimizing a trial wave function with a classical computer . While VQE is celebrated for its ease of use and compatibility with limited quantum hardware, it currently lacks rigorous guarantees regarding timely output production . QPE, on the other hand, is a fault-tolerant algorithm capable of achieving higher accuracy, but it demands significantly greater coherence times and qubit resources, making it less practical for current hardware . The synergy between these algorithms, where VQE can provide good initial approximations for QPE, represents a promising pathway for future quantum chemistry applications . The subsequent sections will delve deeper into the specifics of these concepts, providing a detailed understanding of their contributions to the field of quantum molecular simulation.

2.1 Quantum Representations of Molecular Systems

The initial and crucial step in applying quantum computing to molecular simulation involves representing molecular systems in a format amenable to quantum algorithms. This begins with formulating the molecular electronic structure Hamiltonian in a second-quantized form . The second-quantized Hamiltonian, which utilizes creation ($a^{\dagger}*{p}$) and annihilation ($a*{q}$) operators, is fundamental for describing electron interactions within a molecule, particularly in the context of many-body quantum mechanics . This representation is significant because it implicitly incorporates prior knowledge about the molecule, such as the occupation of electrons in specific energy levels, thereby potentially reducing the number of qubits required for simulation . The occupation number representation, or second-quantized form, is essential for translating fermionic systems, such as electrons, into a qubit-based framework, which is a prerequisite for algorithms like the Variational Quantum Eigensolver (VQE) .

A key challenge in simulating molecular systems on quantum computers arises from the fermionic nature of electrons, which obey the Pauli exclusion principle, a property not intrinsically captured by standard qubits. Therefore, transforming these fermionic systems into qubit systems is a necessary step . This transformation involves mapping fermionic operators (creation and annihilation operators) to qubit operators, typically expressed as Pauli gates. Different transformation techniques exist, each with distinct implications for resource overhead, specifically in terms of qubit count and circuit depth, and their suitability for various molecular Hamiltonians .

One widely recognized transformation technique is the Jordan-Wigner transformation. This method maps fermionic operators to Pauli operators in a straightforward manner, making it conceptually simple to implement . However, a notable disadvantage of the Jordan-Wigner transformation is its introduction of non-local operations, leading to a substantial increase in circuit depth, particularly for systems with many orbitals. This non-locality arises because the transformation requires a "string" of Pauli Z operators for each fermionic mode, coupling distant qubits. Consequently, while conceptually direct, its practical application can incur high circuit depth overhead, which is a significant concern for noisy intermediate-scale quantum (NISQ) devices with limited coherence times.

In contrast to Jordan-Wigner, the Bravyi-Kitaev transformation offers an alternative approach that aims to mitigate the non-locality issue. While not explicitly detailed in the provided digests regarding its mechanics, the Bravyi-Kitaev transformation is known to produce more compact qubit representations and shallower circuits by distributing the non-locality more efficiently across qubits. This often translates to a logarithmic reduction in the number of Pauli strings compared to Jordan-Wigner, leading to potentially fewer gates and shorter circuit depths. This characteristic makes Bravyi-Kitaev potentially more advantageous for larger molecular systems where circuit depth becomes a bottleneck.

Another transformation technique, the parity transformation, is also highlighted for mapping fermionic operators to qubit operators . The parity transformation, similar to Bravyi-Kitaev, seeks to optimize the qubit overhead and circuit depth. Specifically, the use of the parity transformation in certain studies leads to a qubit requirement equal to the number of spin-orbitals . This direct mapping implies an efficient use of qubits, aligning with the goal of reducing resource demands. The parity transformation expresses creation and annihilation operators in terms of Pauli gates, facilitating their implementation on quantum hardware.

The choice of fermion-to-qubit transformation profoundly impacts the feasibility of quantum simulations. The Jordan-Wigner transformation, while conceptually simple, typically results in higher circuit depths due to its non-local character. This can be prohibitive for current quantum hardware, which suffers from decoherence over longer circuit execution times. Conversely, transformations like Bravyi-Kitaev and parity transformations are designed to reduce circuit depth and optimize qubit usage. For instance, the parity transformation directly relates the qubit count to the number of spin-orbitals, suggesting an efficient utilization of quantum resources . This efficiency is critical, as minimizing qubit count and circuit depth directly translates to a higher probability of successful computation on contemporary quantum processors.

In summary, the journey from a molecular system to a quantum simulation begins with its second-quantized representation. This foundational step is followed by the intricate process of transforming fermionic operators into qubit operators. The selection among transformation techniques—such as Jordan-Wigner, Bravyi-Kitaev, or parity transformation—is not merely a technical detail but a critical design choice that dictates the resource overhead (qubit count and circuit depth) and, consequently, the practical feasibility and accuracy of quantum simulations for molecular electronic structure problems. The pursuit of more efficient and less resource-intensive transformations remains a central focus in advancing quantum chemistry applications on quantum computers.

2.2 Variational Quantum Algorithms

The Variational Quantum Eigensolver (VQE) has emerged as a particularly prominent algorithm for molecular simulation, primarily due to its hybrid quantum-classical architecture and its suitability for current noisy intermediate-scale quantum (NISQ) devices . VQE is a heuristic algorithm designed to estimate the ground-state energy of molecular systems, a crucial metric for understanding molecular stability and reactivity, which is fundamental to fields such as drug design . While it is celebrated for its ease of use and compatibility with limited quantum hardware, VQE currently lacks rigorous guarantees regarding the timely production of desired outputs .

The hybrid nature of VQE involves a synergistic interplay between a quantum processor and a classical computer . The quantum component is responsible for preparing a trial wave function, known as an "ansatz," using a parameterized quantum circuit $U(\mathbf{\theta})$ acting on an initial state $|\psi\_0\rangle$. Subsequently, the quantum processor measures the expectation value of the molecular Hamiltonian, $\langle H \rangle = \langle \psi(\mathbf{\theta})|H|\psi(\mathbf{\theta})\rangle$ . According to the variational principle, this expectation value, $E(\theta)$, will always be greater than or equal to the true ground state energy, $E\_0$, i.e., $E(\theta) = \langle \Psi\_{UCC}(\theta) | \hat{H} | \Psi\_{UCC}(\theta) \rangle \ge E\_0$ .

The classical component then takes over, using an optimizer to iteratively adjust the variational parameters $\mathbf{\theta}$ to minimize the energy expectation value obtained from the quantum processor . This iterative optimization process continues until convergence, aiming to find the minimum energy, which approximates the molecular ground state energy . Classical optimizers commonly employed include gradient-based methods such as L-BFGS-B, Adam, or Adagrad, which often necessitate the computation of energy derivatives, typically achieved using techniques like the parameter-shift rule . Tools like the MindSpore Quantum framework facilitate this process by offering automatic differentiation capabilities, akin to those found in machine learning frameworks .

A critical aspect of VQE's performance is the choice of the quantum ansatz, which dictates the form and complexity of the trial wave function. The ansatz profoundly influences the accuracy, expressivity, and resource requirements of the VQE algorithm. An ideal ansatz should be expressive enough to capture the true ground state with high fidelity, yet trainable to avoid issues like barren plateaus, and resource-efficient to be implementable on current or near-term quantum hardware .

One prominent type of ansatz used in VQE for molecular systems is the Unitary Coupled Cluster Single and Double excitations (UCCSD) ansatz . Inspired by classical coupled cluster theory, UCCSD is highly expressive, capable of accurately describing electron correlation, which is vital for molecular electronic structure calculations. Its expressivity stems from its ability to generate quantum states that closely approximate the exact ground state wave function, making it a powerful choice for achieving high accuracy in early molecular simulations . However, this high expressivity comes with increased complexity and resource demands, requiring a greater number of quantum gates and parameters, which can challenge the trainability on NISQ devices due to potential issues like barren plateaus and increased noise susceptibility.

In contrast to highly expressive, problem-inspired ansätze like UCCSD, hardware-efficient ansätze are designed to be tailored to specific quantum hardware architectures. These ansätze often consist of layers of alternating single-qubit rotations and entangling gates (e.g., CNOTs), designed to be shallow and minimize circuit depth. Their primary advantage lies in their reduced resource requirements, making them more amenable to current noisy quantum computers. However, their lower expressivity can limit their ability to accurately represent complex molecular wave functions, potentially leading to less accurate ground state energy estimations .

The choice between different ansatz types in VQE involves a fundamental trade-off between complexity and accuracy. While UCCSD offers superior accuracy due to its strong theoretical grounding and high expressivity, it demands significant quantum resources, potentially limiting its practical application on current quantum hardware. Hardware-efficient ansätze, conversely, are more resource-friendly and trainable on NISQ devices but may yield lower accuracy. For early molecular simulations, this trade-off is critical. Researchers must consider the specific molecular system, available quantum hardware capabilities, and desired accuracy when selecting an ansatz. Future advancements in quantum hardware and error mitigation techniques may bridge this gap, enabling the use of more complex and accurate ansätze like UCCSD for larger molecular systems. This continuous advancement aims to integrate the strengths of quantum and classical computing, akin to hybrid approaches leveraging Density Matrix Embedding Theory (DMET) with Sample-Based Quantum Diagonalization (SQD) for efficient molecular simulations . Overall, VQE represents a promising pathway for quantum chemistry, offering a method to find low-energy states that can be further refined, potentially by methods like Quantum Phase Estimation (QPE), to achieve perfect ground states .

3. Early Applications and Demonstrations in Molecular Simulation

This section reviews the foundational demonstrations of quantum computing in molecular simulation and materials science, detailing the specific molecular systems and material properties investigated, alongside the chemical and physical properties calculated . The applications are categorized by the nature of the problem addressed, encompassing small molecule ground state energy calculations, initial explorations of reaction mechanisms, and the prediction of material properties . We synthesize observed trends in the types of molecules and properties simulated, highlighting common challenges encountered across these early demonstrations and comparing findings to identify corroborating or conflicting results and overarching patterns.

Section 3.1, "Molecular Electronic Structure Calculations and Properties," delves into the initial successes of quantum algorithms, particularly the Variational Quantum Eigensolver (VQE), in calculating fundamental molecular properties such as ground state energies. It presents specific comparative data, including accuracy metrics and computational resource usage for simulated molecules, benchmarked against classical computational chemistry methods like Full Configuration Interaction (FCI), Coupled Cluster Singles and Doubles (CCSD), and Hartree-Fock (HF) . This sub-section critically evaluates the limitations and specific use cases where quantum methods currently excel or fall short compared to classical benchmarks, analyzing the types of errors observed and their origins, explicitly linking them to the constraints of Noisy Intermediate-Scale Quantum (NISQ) hardware. It synthesizes how quantum computing offers the potential for more precise and rapid simulations, especially for complex molecular modeling, which is essential for understanding molecular properties and advancing fields like drug discovery .

Section 3.2, "Simulation of Larger and More Complex Molecules and Materials," broadens the scope to examine efforts aimed at simulating larger and more complex molecular systems and materials. It assesses the scalability of algorithmic innovations designed to mitigate hardware limitations, such as decomposition methods that reduce qubit requirements and advanced VQE variants like ADAPT-VQE and Overlap-ADAPT-VQE . This sub-section explores how insights from error mitigation techniques, even if not explicitly defined as quantum error correction codes, are implicitly applied to enhance the robustness of these simulations against hardware noise. It discusses the transition from simple diatomic molecules to hydrogen chains, cyclohexane conformers, and industrially relevant materials, assessing the current feasibility and future prospects of quantum simulations for complex chemical and material science problems .

3.1 Molecular Electronic Structure Calculations and Properties

Quantum computing has emerged as a promising avenue for addressing the inherent challenges in molecular electronic structure calculations, a cornerstone of computational chemistry and drug discovery . Classical methods often struggle with accurately simulating systems involving many entangled or superimposed particles, particularly for larger molecules like proteins or drug compounds, leading to computational bottlenecks and limitations in achieving high precision . In this context, algorithms such as the Variational Quantum Eigensolver (VQE) have been extensively explored for determining the ground state energies and other fundamental molecular properties.

Early case studies have demonstrated the application of VQE and similar algorithms to calculate the electronic structure of small molecules. For instance, VQE has been successfully applied to molecules such as H₂, LiH, BeH₂, and even hydrogen chains up to H₁₂ . IBM's Qiskit Chemistry module, for example, has facilitated proof-of-concept experiments for molecules like LiH, BeH₂, and H₂O, aiming to validate the feasibility of quantum simulations for understanding molecular interactions at an atomic level .

A significant demonstration of VQE's capabilities is the calculation of the ground state energy for the LiH molecule. One study utilized the STO-3G basis set and a Unitary Coupled-Cluster with Singles and Doubles (UCCSD) ansatz, requiring 12 qubits and 640 parameter gates (44 variational parameters). The optimized VQE energy was reported as -7.8823528289794922 Ha, which is remarkably close to the classically obtained Full Configuration Interaction (FCI) energy of -7.8823622867987249 Ha, indicating high accuracy .

For comparison, the Hartree-Fock (HF) energy was -7.8633576215351200 Ha and the Coupled Cluster Singles and Doubles (CCSD) energy was -7.8823529091527051 Ha. This highlights VQE's ability to approach the exact FCI solution for small systems, a benchmark for electronic structure methods .

Further applications of VQE include calculations for $H\_3^+$, $OH^-$, $HF$, and $BH\_3$ molecules using the STO-3G basis set and parity transformation for fermion-to-qubit mapping. These simulations utilized between 6 and 16 qubits. The results showed good agreement with FCI calculations, particularly at equilibrium bond lengths, and in some cases, achieved higher accuracy than previously reported values for similar molecules, which was attributed to not using significant qubit reductions . These examples underscore the potential of VQE to achieve high precision in ground state energy calculations, crucial for predicting binding affinities and understanding drug-target interactions .

Beyond ground state energies, quantum algorithms are also being developed for calculating molecular forces and energy gradients. New quantum algorithms have been proposed to significantly reduce the complexity of these calculations, with techniques for NISQ devices focusing on reducing circuit repetitions through low-rank factorizations and optimized tomography schemes. For fault-tolerant quantum computing, methods for estimating energy derivatives with Heisenberg-limited scaling are being explored, which could lead to costs comparable to energy estimation for chemical systems . While specific comparative data on accuracy for forces was not provided, the focus on complexity reduction indicates a path towards more efficient gradient computations.

A significant achievement in simulating larger molecular systems with high accuracy was demonstrated on an IonQ trapped-ion quantum computer. This method achieved chemical accuracy when applied to a 10-hydrogen atom ring, a critical benchmark for electronic structure methods. The results were compared to classical FCI calculations, reinforcing the quantum computer's ability to provide exact solutions for systems beyond the reach of classical exact methods . Another notable development is the application of the DMET-SQD hybrid method to calculate properties of an 18-hydrogen atom ring and various conformers of cyclohexane. This method achieved energy differences between cyclohexane conformers within 1 kcal/mol of established classical reference methods like Coupled Cluster Singles and Doubles with perturbative triples and Heat-Bath Configuration Interaction (HCI). The SQD method also exhibited tolerance to noise, which mitigated errors on current quantum hardware, preserving the correct energy ordering of cyclohexane conformers and matching HCI benchmarks for the hydrogen ring .

Despite these successes, early quantum demonstrations for molecular simulation face several limitations, predominantly linked to the characteristics of Noisy Intermediate-Scale Quantum (NISQ) hardware. Noise effects on energy calculations are a pervasive challenge, necessitating the implementation of error mitigation strategies, such as enforcing physical symmetries and N-representability conditions . The complexity of mapping fermionic Hamiltonians to qubits and the substantial number of operations still required for even moderately sized molecules often exceed the capabilities of current quantum computers . The depth and number of gates in quantum circuits, such as the 12612 total gates for the LiH simulation, hint at significant resource demands . These limitations manifest as inaccuracies or increased computational demands compared to highly optimized classical methods like Density Functional Theory (DFT), Configuration Interaction (CI), and Quantum Monte Carlo (QMC), especially for larger systems where classical heuristics currently outperform quantum approaches due to hardware constraints . The exact calculation of ground states is generally NP-hard, implying that heuristic quantum methods, similar to their classical counterparts, are more likely to yield practical results in the near term .

Quantum methods currently excel in their theoretical promise for high-precision calculations that are intractable for classical computers, particularly for systems with strong electron correlation or those requiring exact solutions. While classical methods like FCI offer exact solutions, their computational cost severely limits their applicability to very small molecules. Quantum computing offers a path to extending this exactness to larger, more complex systems. Pseudopotentials are being explored to simplify the simulation of atomic core interactions, reducing computational costs for quantum simulations, as shown in modeling carbon monoxide adsorption where accuracy was comparable to traditional methods but still required substantial operations beyond current hardware capabilities .

In summary, while quantum algorithms like VQE have demonstrated their capability to achieve high accuracy for small molecular systems, often reaching chemical accuracy comparable to or surpassing advanced classical methods like CCSD and approaching FCI, current NISQ hardware limitations such as noise and qubit availability restrict their immediate practical applicability to larger, more complex systems. The types of errors encountered are primarily due to hardware noise and decoherence, leading to deviations from ideal quantum mechanical behavior. Despite these challenges, the unique ability of quantum computers to handle entangled and superimposed states positions them to enable more precise and rapid simulations, especially for complex molecular modeling crucial for drug discovery and material science, offering a future where quantum simulations can unlock deeper insights into molecular properties and interactions . The development of fault-tolerant quantum computing and continued improvements in NISQ error mitigation strategies are critical for realizing this potential.

3.2 Simulation of Larger and More Complex Molecules and Materials

Quantum computing is increasingly being applied to material science, particularly for simulating complex material properties that are beyond the reach of classical computational methods. This advancement is driven by the potential to explore properties of materials with complex, non-cubic structures , which are common in real-world applications. The ultimate goal is to facilitate innovations such as high-temperature superconductors and more resilient electronics by understanding and predicting material properties at the atomic level .

Significant progress has been made in simulating larger molecular systems and complex material systems. Early milestones include the simulation of hydrogen chains up to H₁₂ using 12 qubits by Google . More recently, molecular systems such as hydrogen rings and cyclohexane conformers, which are more complex than simple diatomic molecules, have been successfully simulated . Similarly, small-scale proofs of concept have demonstrated the simulation of larger molecules like caffeine or penicillin precursors . IBM is actively collaborating with pharmaceutical firms to scale these methods for more intricate, drug-like molecules .

These advances are supported by various algorithmic innovations and computational resources. A notable approach involves decomposing large molecular problems into smaller subproblems, which significantly reduces the required number of qubits, potentially by a factor of 10, while maintaining accuracy .

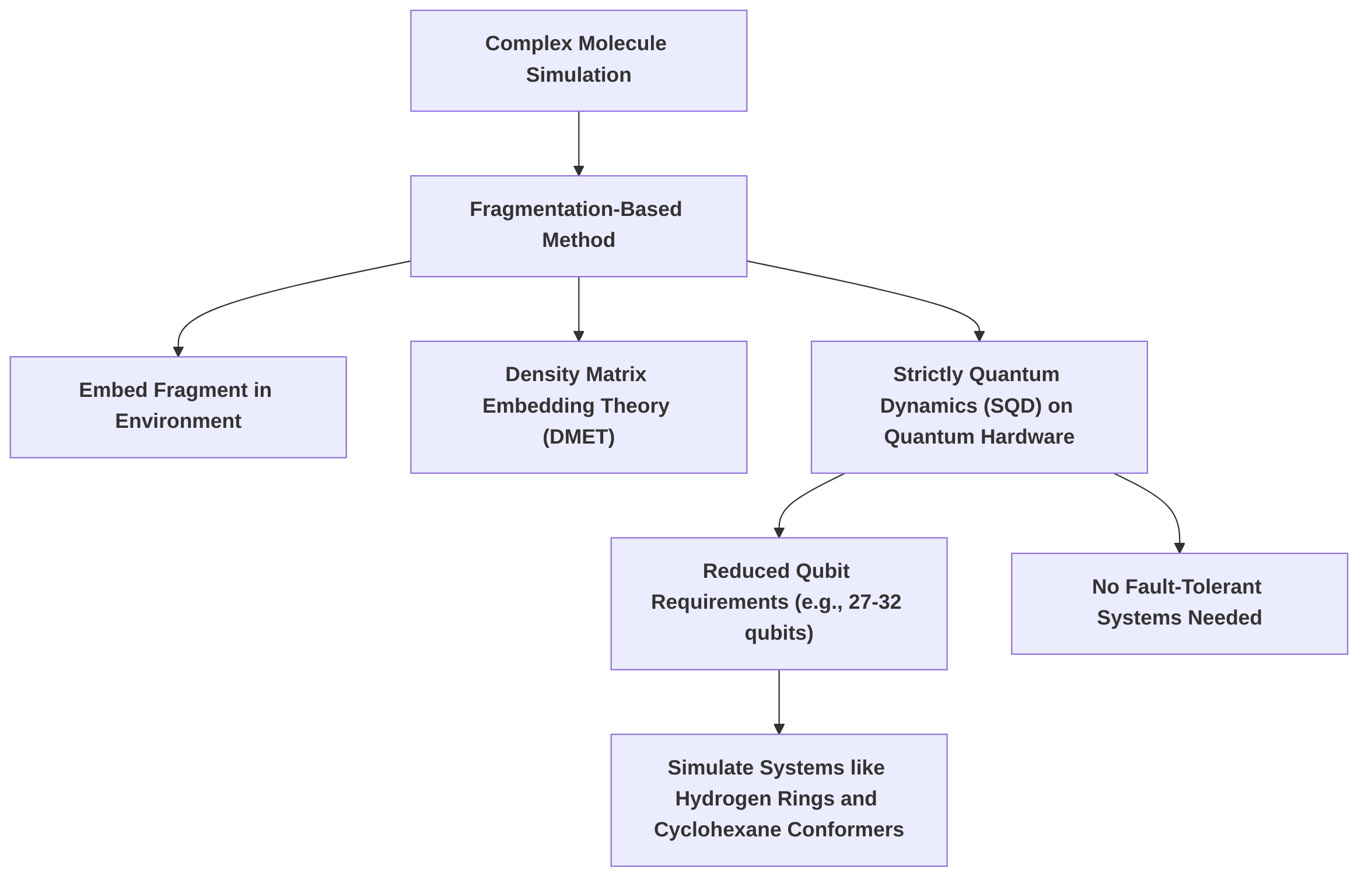
This fragmentation-based method, exemplified by embedding chemically relevant fragments within an approximate electronic environment using Density Matrix Embedding Theory (DMET) and solving them with Strictly Quantum Dynamics (SQD) on quantum hardware, allows for the simulation of systems like hydrogen rings and cyclohexane conformers with a limited number of qubits (27-32) without demanding fault-tolerant quantum systems . Such an approach makes it feasible to simulate industrially relevant molecular compounds, which would otherwise require thousands of qubits .

Another crucial algorithmic innovation is the development of ADAPT-VQE (Adaptive Derivative-Assembled Problem-Tailored Variational Quantum Eigensolver) and its variant, Overlap-ADAPT-VQE. These methods systematically and efficiently construct ansätze, which are essential for handling the complexity of larger systems . IBM's 100-qubit Schwinger model simulation, using ADAPT-VQE with operator decoherence renormalization, represents a significant achievement in managing larger systems while mitigating noise . While the primary focus of some research is on developing efficient algorithms for calculating energy derivatives (forces and gradients) for any molecular system to reduce computational cost , these innovations are foundational for enabling dynamic simulations of complex systems.

The scalability of these innovations is a critical concern, as they attempt to mitigate current hardware limitations. For instance, the adapted pseudopotential method allows for the efficient encoding of pseudopotentials into a format suitable for quantum hardware, reducing both qubit count and computational steps. However, even with these improvements, the quantum resources required for certain reactions, such as carbon monoxide adsorption, remain substantial, demanding billions of operations that are beyond current quantum computer capabilities . This highlights a persistent gap between current hardware capabilities and the demands of complex chemical simulations.

Current quantum hardware platforms, such as IBM's superconducting qubits and IonQ's trapped-ion systems, are actively being leveraged. IonQ's trapped-ion quantum computer has been instrumental in demonstrating the subproblem decomposition approach for larger molecular systems . While current IonQ Forte systems have 36 qubits, next-generation systems are anticipated to have "hundreds of millions of qubits," indicating a clear path toward overcoming scale limitations . However, some existing research, such as the VQE application for the LiH molecule, relies on a relatively small number of qubits (12 qubits, 12612 gates), and does not specifically detail external hardware platforms like IonQ, focusing instead on internal framework efficiencies like MindSpore Quantum . This demonstrates that while specialized hardware continues to evolve, the development of efficient quantum algorithms remains crucial for practical applications.

The field is also exploring the potential for simulating complex material properties beyond simple molecular systems. Applications extend to industrially relevant materials, which are difficult to characterize due to their large number of electrons. Simplified models, requiring fewer qubits, are being developed for studying magnetic materials and high-temperature superconductors . Furthermore, quantum computers are posited to excel in understanding multi-metal systems found in enzymes like P450 and FeMoco, relevant to drug binding affinities and biological ammonia production . Other proposed applications include exploring Type-II superconductivity, searching for high-temperature superconducting materials, photocatalytic reactions for hydrogen fuel, carbon capture, efficient solar cells, and higher-capacity batteries . The simulation of material properties like the metal-insulator transition and antiferromagnetic order in the Hubbard model has also been targeted using VQE on superconducting qubits .

While specific error mitigation techniques derived from quantum error correction codes in information theory are not extensively detailed within the provided digests, the emphasis on robust algorithms like ADAPT-VQE with operator decoherence renormalization for noise control and the ability to operate without requiring fault-tolerant quantum systems implicitly address the challenge of reducing noise in molecular simulations. The current focus remains on developing algorithms that are resilient to the noise prevalent in Noisy Intermediate-Scale Quantum (NISQ) devices, often through careful ansatz construction and variational optimization. Future error-corrected quantum computers are anticipated to be first deployed in industrial R&D for applications in complex systems, highlighting the long-term vision for quantum computing in materials science and chemistry .

4. Quantum Computing in Drug Discovery and Development

Quantum computing is poised to transform drug discovery and development by extending beyond fundamental molecular simulation into practical applications, addressing critical challenges within the drug development pipeline . This paradigm shift is driven by the unique ability of quantum approaches to model complex molecular interactions and biological systems with unprecedented accuracy and efficiency, often surpassing the capabilities of classical computational methods. The integration of quantum computing in this field aims to significantly accelerate the identification of viable drug candidates, enhance the understanding of drug-target interactions, and streamline various stages from lead discovery to clinical trials.

The following subsections will delve into two primary avenues through which quantum computing is impacting drug discovery. Specifically, Section 4.1, "Quantum Simulation for Molecular Properties in Drug Discovery," will focus on the direct application of quantum simulation techniques to precisely model molecular behavior. This includes an analysis of how quantum algorithms, such as Quantum Phase Estimation (QPE) and the Variational Quantum Eigensolver (VQE), are adapted and extended for tasks like accurate energy calculations, conformational sampling, and predicting binding affinities. A critical aspect of this discussion will be the comparison of the accuracy and efficiency of these quantum simulations against established classical methodologies for drug-related molecules, highlighting their theoretical advantages in handling complex electronic structures and electron correlations .

Subsequently, Section 4.2, "Quantum Machine Learning and Advanced Applications in Drug Discovery," will explore the broader impact of quantum-enhanced machine learning (QML) approaches. This section will cover how QML models are being applied to tackle complex challenges such as protein folding, ADMET (Absorption, Distribution, Metabolism, Excretion, and Toxicity) prediction, and de novo drug design. It will analyze the potential impact and current challenges of these quantum-enhanced ML approaches, linking them to their relevance within broader drug development pipelines . Furthermore, this section will critically compare the suitability of various quantum-enhanced ML algorithms, such as Quantum Support Vector Machines (QSVM), Quantum Principal Component Analysis (QPCA), Quantum Generative Adversarial Networks (QGANs), and Quantum Approximate Optimization Algorithm (QAOA), for accelerating specific drug discovery workflows, including clinical trial optimization . Throughout these discussions, relevant case studies and partnerships, such as the collaboration between IonQ and AstraZeneca, will illustrate the practical integration and potential of quantum computing in drug development .

4.1 Quantum Simulation for Molecular Properties in Drug Discovery

Quantum computing presents a transformative approach to overcoming the inherent challenges in drug discovery by enabling highly accurate and efficient molecular simulations . Traditional drug discovery is often hampered by the complexity of molecular interactions, the vastness of chemical space, and the computational intensity required for accurate predictions of molecular behavior. Quantum simulation is poised to address these issues by modeling molecular interactions at an atomic level with unprecedented precision and speed, thereby accelerating the identification of viable drug candidates and enhancing the understanding of how compounds interact with biological systems .

One of the primary challenges in drug discovery that quantum computing aims to tackle is the accurate prediction of drug-target interactions, particularly binding affinities and specificity . Understanding these interactions at an atomic level, including charge distribution and orbital overlap, is fundamental for designing effective drugs . Classical methods often struggle with the precise calculation of electronic structures, which are critical for determining these properties. Quantum solutions, such as those employing Quantum Phase Estimation (QPE) for Density Functional Theory (DFT) calculations and Quantum Amplitude Estimation (QAE), are envisioned to provide significantly improved accuracy in predicting binding affinities by directly solving electronic structure problems . For instance, QPE is explored for exact energy eigenvalues, offering a pathway to model ground state energies with enhanced precision, which is crucial for understanding molecular stability and reactivity in drug design .

The Variational Quantum Eigensolver (VQE) is a prominent hybrid quantum-classical algorithm that is being adapted and tailored to address these specific drug discovery challenges. VQE is particularly effective for estimating ground-state energies of molecules, which is foundational for drug design by determining molecular stability and reactivity . Beyond ground-state energy, VQE is also discussed for molecular structure optimization, binding affinity prediction, and electronic structure calculations, with its more accurate variant, Quantum Chemistry Compilation (QCC), being considered for electron correlations . These capabilities aim to improve the accuracy and efficiency of identifying drug candidates and understanding their interactions, potentially reducing the time from years to days for complex protein-ligand interactions .

Furthermore, quantum computing offers theoretical advantages over classical methods in simulating complex molecular systems like proteins and enzymes. While classical simulations are limited by computational resources, quantum computers can model molecular behavior at an atomic level with unprecedented accuracy and speed, predicting how compounds interact with biological systems . This scalability allows for the study of larger, more intricate biological systems critical for understanding compound interactions and predicting molecular behavior . For example, simulations of adenosine triphosphate (ATP) function and ibuprofen's function have been accurately predicted using quantum approaches, demonstrating their immediate applicability .

Another critical area is the optimization of drug modality and properties, including specificity, binding affinity, and ADMET (Absorption, Distribution, Metabolism, Excretion, and Toxicity) characteristics . Quantum computing can provide more effective and efficient simulations of quantum mechanical interactions between compounds and proteins, thereby improving the prediction of these crucial properties. Additionally, it holds potential for improving predictions of drug molecules' unbinding kinetics (K_off), which could lead to better dosing regimens .

Hybrid quantum-classical algorithms are also being tested to accelerate conformational sampling and improve scoring accuracy in virtual screening, allowing for the simulation of multi-target binding or metabolic pathways . An illustrative example of how quantum simulation tools could be applied to complex chemical problems relevant to drug design is the Suzuki-Miyaura reaction, a key method for synthesizing small-molecule pharmaceuticals. Accelerating simulations of reaction steps within such processes can significantly help researchers narrow down viable drug candidates earlier in the discovery pipeline . The ability to accurately simulate such reactions and complex molecular interactions could lead to breakthroughs in treating diseases and testing compound effectiveness or toxicity .

The theoretical advantages of quantum simulations stem from their ability to inherently handle the quantum mechanical nature of molecular interactions, which is approximated in classical simulations. This allows for a more accurate representation of electron correlations, charge distributions, and orbital overlaps that dictate chemical reactivity and binding. For instance, understanding multi-metal systems, relevant for calculating ligand binding affinities in drugs, is an area where quantum computers could significantly contribute . This enhanced accuracy and efficiency promise to reduce the time and cost associated with traditional drug development, opening new avenues for medical advancements and improving our ability to understand and treat disease by predicting molecular behavior more effectively .

4.2 Quantum Machine Learning and Advanced Applications in Drug Discovery

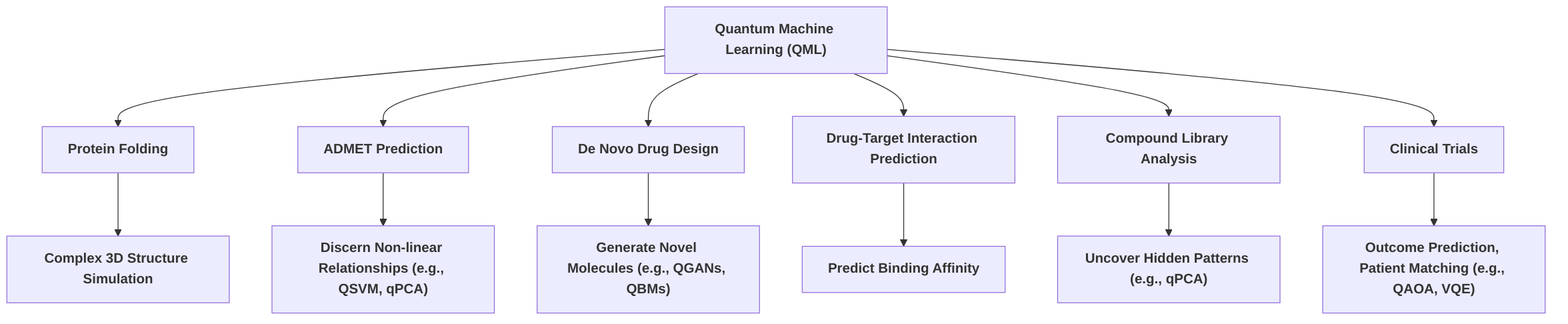
Quantum computing is poised to address several formidable challenges in drug discovery through the integration of quantum machine learning (QML) and other advanced applications, offering theoretical advantages over classical methodologies . These applications extend beyond direct molecular simulation to encompass complex biological and chemical problems, leveraging the inherent capabilities of quantum mechanics to process and analyze data in ways intractable for classical computers. The synergy between quantum computing and artificial intelligence (AI) is particularly highlighted, where AI analyzes data from quantum simulations to identify patterns crucial for drug development, predict potential side effects, and even enable personalized medicine by simulating individual patient responses . This hybrid approach aims to drastically reduce costs and accelerate the time-to-market for novel drugs by enhancing pattern recognition in large datasets and improving the efficiency of generative modeling .

One significant challenge quantum computing is tackling is protein folding, a process fundamental to understanding disease mechanisms and designing targeted therapies . Proteins, implicated in numerous serious diseases, adopt complex three-dimensional structures that determine their function. Classical methods struggle to simulate protein folding with high fidelity due to the exponential growth of conformational space with protein size. Quantum computing models are envisioned to simulate protein folding with exceptional accuracy, predicting stable structures and essential cellular interactions, thereby providing deep molecular insights invaluable for deciphering disease mechanisms and developing therapies that precisely interact with biological structures . While specific QML models for protein folding are still nascent, the capability for high-fidelity quantum simulation underpins this application.

Another critical area is ADMET (Absorption, Distribution, Metabolism, Excretion, and Toxicity) prediction, which is crucial for assessing drug safety and pharmacokinetics early in the discovery pipeline. Quantum Machine Learning (QML) models are employed to discern intricate, nonlinear relationships within molecular descriptor spaces, potentially identifying patterns beyond the reach of classical algorithms . Specifically, Quantum Principal Component Analysis (QPCA) can be utilized for feature reduction to streamline data, while Quantum Support Vector Machines (QSVM) are proposed for classification tasks related to small-molecule ADMET prediction . These QML approaches promise improved accuracy and reduced computational overhead in predicting crucial ADMET properties, leading to more reliable drug candidates .

De novo drug design, the process of generating novel molecular structures with desired physicochemical properties, stands to benefit immensely from quantum advancements. Quantum generative models, such as quantum Boltzmann machines (QBMs), variational autoencoders, and Quantum Generative Adversarial Networks (QGANs), can explore vast chemical spaces to design new molecules with tailored characteristics . This allows for the generation of molecular structures that are difficult or impossible to conceive using traditional methods, potentially accelerating the identification of lead compounds. The convergence of generative chemistry, an AI/ML-driven component of computer-aided drug design (CADD), with quantum computing's precision is expected to significantly enhance drug discovery workflows .

Drug-target interaction prediction, which aims to determine how strongly a drug candidate binds to its biological target, is another area where QML methods are proposed to predict binding affinity . Accurate prediction of binding affinity is paramount for identifying potent and selective drug candidates. Quantum Neural Networks (QNNs), Quantum Kernel Methods, and QBMs are broadly mentioned for their potential in these drug design tasks, including predicting molecular activity and modeling complex interactions .

Furthermore, compound library analysis can be optimized using quantum algorithms. Quantum k-means algorithms and Quantum Principal Component Analysis (qPCA) are leveraged to uncover hidden substructures and relationships within large compound libraries . This capability is crucial for scaffold hopping, a strategy used to replace existing molecular scaffolds with novel ones while retaining or improving biological activity, and for lead optimization, the process of improving the properties of a lead compound. The ability to identify subtle patterns in vast datasets can significantly accelerate the selection of promising candidates.

Beyond these specific applications, QML extends into the realm of clinical trials. Quantum algorithms are being explored for outcome prediction (e.g., using QSVMs and QNNs), patient recruitment and matching (using QSVMs and QNNs to analyze electronic health records), and site selection/ranking (using Quantum Approximate Optimization Algorithm (QAOA) and Variational Quantum Eigensolver (VQE) for optimization) . The Quantum Approximate Optimization Algorithm (QAOA) is also specifically noted as a tool for optimizing parameters in drug design, particularly for identifying effective molecular configurations . Collaborations, such as Roche's investigation into quantum computing for Alzheimer's research, exemplify the early adoption of these technologies to improve the simulation of complex protein interactions, like those involving amyloid-beta .

In summary, the adaptation of fundamental quantum algorithms like QSVM, QPCA, QNN, QBM, QGAN, and hybrid approaches like QAOA and VQE, is tailored to address the nuances of specific drug discovery challenges . These quantum solutions offer theoretical advantages in terms of accuracy, computational efficiency, and the ability to explore complex spaces that are classically intractable. The potential for improved accuracy and reduced computational cost is a recurring theme across these advanced applications . While still in early stages, the integration of quantum computing with AI and ML is poised to revolutionize various aspects of the drug discovery pipeline, from molecular design to clinical trial optimization .

5. Challenges and Limitations of Early Applications

The early adoption of quantum computing for molecular simulations has been significantly hampered by a confluence of hardware, algorithmic, and software constraints, coupled with the nascent stage of the technology itself.

A critical deficiency lies in the hardware, specifically the Noisy Intermediate-Scale Quantum (NISQ) devices, which are characterized by a limited number of qubits, high error rates, short coherence times, and extreme susceptibility to environmental noise . This noise fundamentally compromises computational accuracy, necessitating robust error correction mechanisms, which themselves require significant scientific and engineering breakthroughs for stabilizing and manipulating qubits . Current quantum processors often have limited qubit counts, such as IonQ Forte with 36 qubits, making it challenging to simulate industrially relevant molecules which may require over 2000 qubits . The need for specialized conditions, such as ultra-low temperatures and advanced cryogenic systems, further exacerbates the scalability obstacle . The underlying cause of these hardware limitations stems from the delicate nature of quantum phenomena, where interactions with the environment lead to decoherence, preventing qubits from reliably holding their quantum states .

Algorithmic challenges present another significant barrier, particularly concerning the efficiency and reliability of quantum algorithms in the NISQ era. While Variational Quantum Eigensolver (VQE) is a popular heuristic algorithm, it notably lacks rigorous guarantees . Its practical application demands efficient implementations and careful optimization, with circuits for UCCSD ansatze involving a substantial number of gates and parameters (e.g., 12612 gates and 44 parameters for LiH), making it computationally intensive .

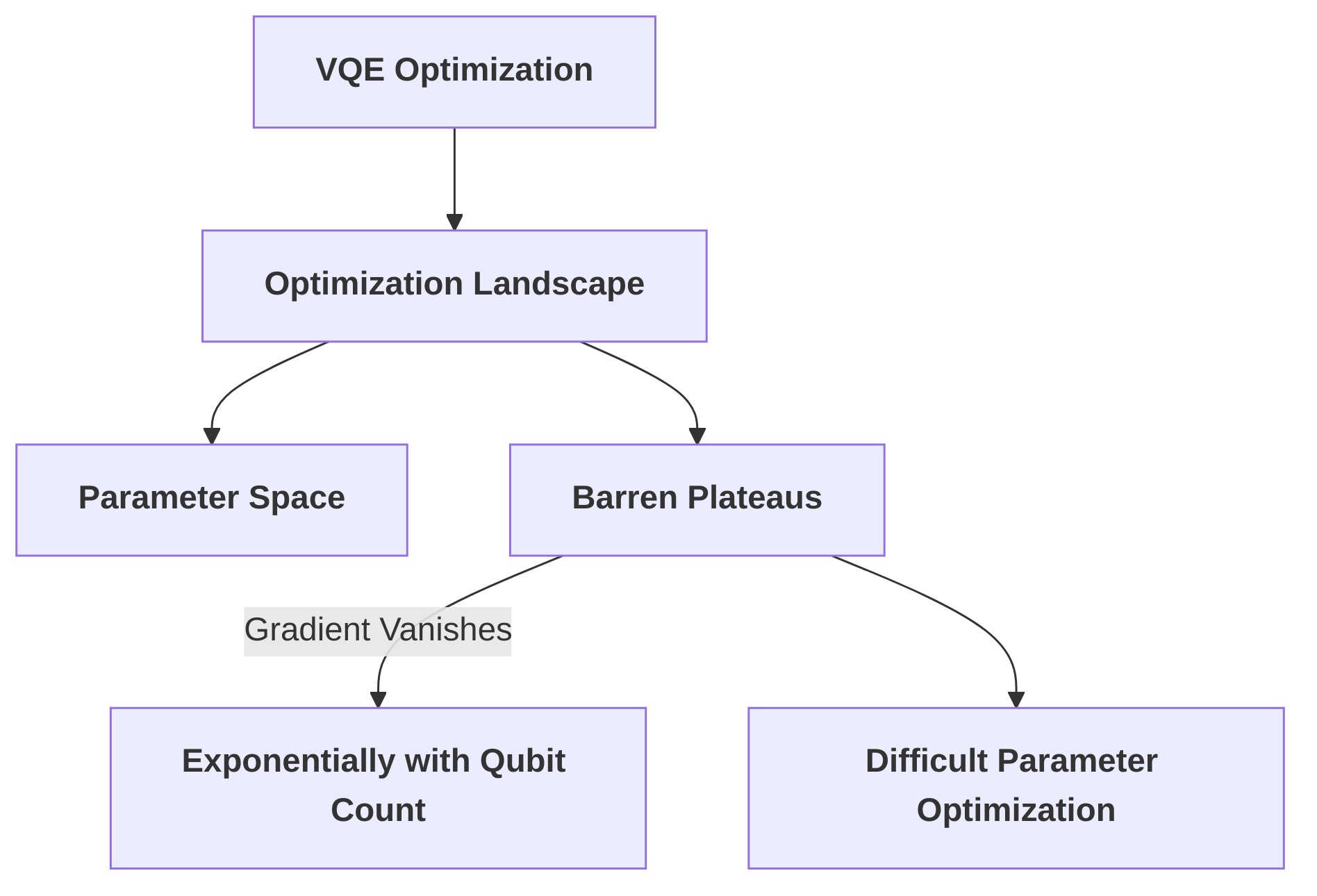
A critical issue within VQE is the susceptibility to "barren plateaus," which are regions in the optimization landscape where gradients vanish exponentially with the number of qubits, making parameter optimization exceedingly difficult . While not explicitly named in all digests, the implication of optimization difficulties with hardware-efficient ansätze points to this inherent problem . Furthermore, algorithms like Quantum Phase Estimation (QPE), while theoretically powerful, require substantial resources, including significant gate depth and a large number of qubits, making them impractical for current NISQ devices . The computational cost and complexity of calculating energy derivatives, essential for molecular dynamics simulations, also pose significant hurdles, despite ongoing efforts to reduce resource requirements through algorithmic optimization . The root cause of these algorithmic challenges often lies in the classical optimization components of hybrid quantum-classical algorithms, where the vast parameter spaces of quantum circuits lead to difficult optimization landscapes and substantial classical pre- and post-processing overhead .

Beyond hardware and algorithmic specifics, several overarching limitations underscore the "early stage" nature of quantum computing in molecular simulation. The concept of "quantum advantage" – where quantum computers definitively outperform classical ones for practical, industrially relevant problems – remains largely a future goal . Skepticism regarding the timely applicability for urgent global challenges like climate change stems from the mismatch in timelines, with significant quantum utility unlikely before the 2030s . Achieving fault tolerance, essential for reliable commercial use, is identified as a primary technical hurdle due to quantum decoherence and noise . Current systems are too prone to error to achieve practical quantum value . Logistical challenges include scaling quantum hardware, developing specialized quantum algorithms tailored for life sciences, and navigating regulatory and ethical issues related to data privacy . The integration of quantum computing into existing R&D pipelines also presents practical hurdles due to the need for seamless interoperability with classical tools and a lack of standardized frameworks and benchmarking protocols . Furthermore, the interdisciplinary nature of quantum computing for molecular simulation leads to a scarcity of talent, which is a significant hindrance to progress .

To address these multifaceted challenges, future research must focus on several critical areas. In the hardware domain, solutions involve developing more robust and reliable quantum processors with increased qubit counts and improved coherence times. This necessitates breakthroughs in quantum error correction to mitigate the effects of noise and achieve fault tolerance . Algorithmic advancements should prioritize developing more efficient ansätze for VQE that are less susceptible to barren plateaus, perhaps through adaptive methods like ADAPT-VQE . Research into resource-efficient quantum algorithms for tasks like QPE and energy derivative calculations is also crucial . Solutions like problem decomposition, which reduces qubit requirements for larger molecules, represent promising avenues . Hybrid quantum-classical approaches, where classical supercomputers assist with error correction and optimization, serve as a pragmatic bridge for current NISQ devices, demonstrating improved simulation times compared to purely classical methods . Software development must focus on sophisticated tools that enable seamless integration with classical workflows, standardization of frameworks, and robust benchmarking protocols to objectively assess quantum advantage . Finally, fostering interdisciplinary talent and establishing clear regulatory and ethical guidelines will be vital for the responsible and widespread adoption of quantum computing in molecular simulation . These identified challenges are not merely limitations but rather critical areas that future research must intensively address to transition quantum computing from its current nascent stage to one of practical utility and transformative impact.

6. Ethical Considerations and Societal Impact of Quantum Molecular Simulation

The advancement of quantum molecular simulation, particularly its application in drug discovery, presents a complex array of ethical considerations and societal impacts that extend beyond purely technical discussions . While many papers focus solely on the technical aspects of quantum computing for molecular simulation, such as the application of Variational Quantum Eigensolver (VQE) in quantum chemistry , or the potential to accelerate drug development timelines , a critical examination of its broader implications is essential for responsible development.

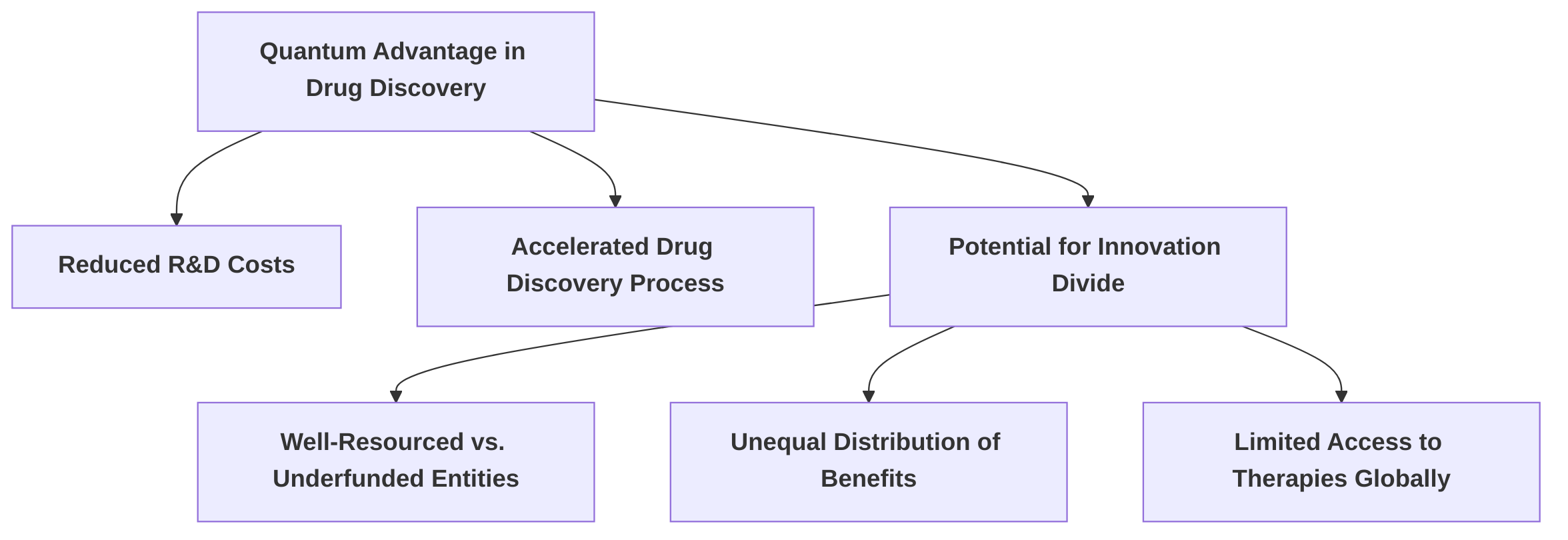
A primary concern revolves around the economic implications of quantum advantage in drug discovery. Quantum computing has the potential to significantly reduce research and development costs, thereby accelerating the drug discovery process and enhancing the ability to understand and treat diseases . However, the substantial upfront investment required for quantum infrastructure and expertise could widen the gap between well-resourced institutions and underfunded entities . This disparity risks creating an innovation divide, where only a select few possess the capability to leverage these powerful simulation tools, leading to an unequal distribution of benefits and potentially limiting access to breakthrough therapies globally, particularly for wealthier nations over developing ones .

Ethical dimensions also emerge concerning data integrity, transparency, and fairness, especially in Quantum Machine Learning (QML) models utilized for drug design. QML models often operate as "black boxes," making their internal workings and decision-making processes difficult to interpret and validate . This lack of transparency raises concerns about accountability and the potential for algorithmic bias.

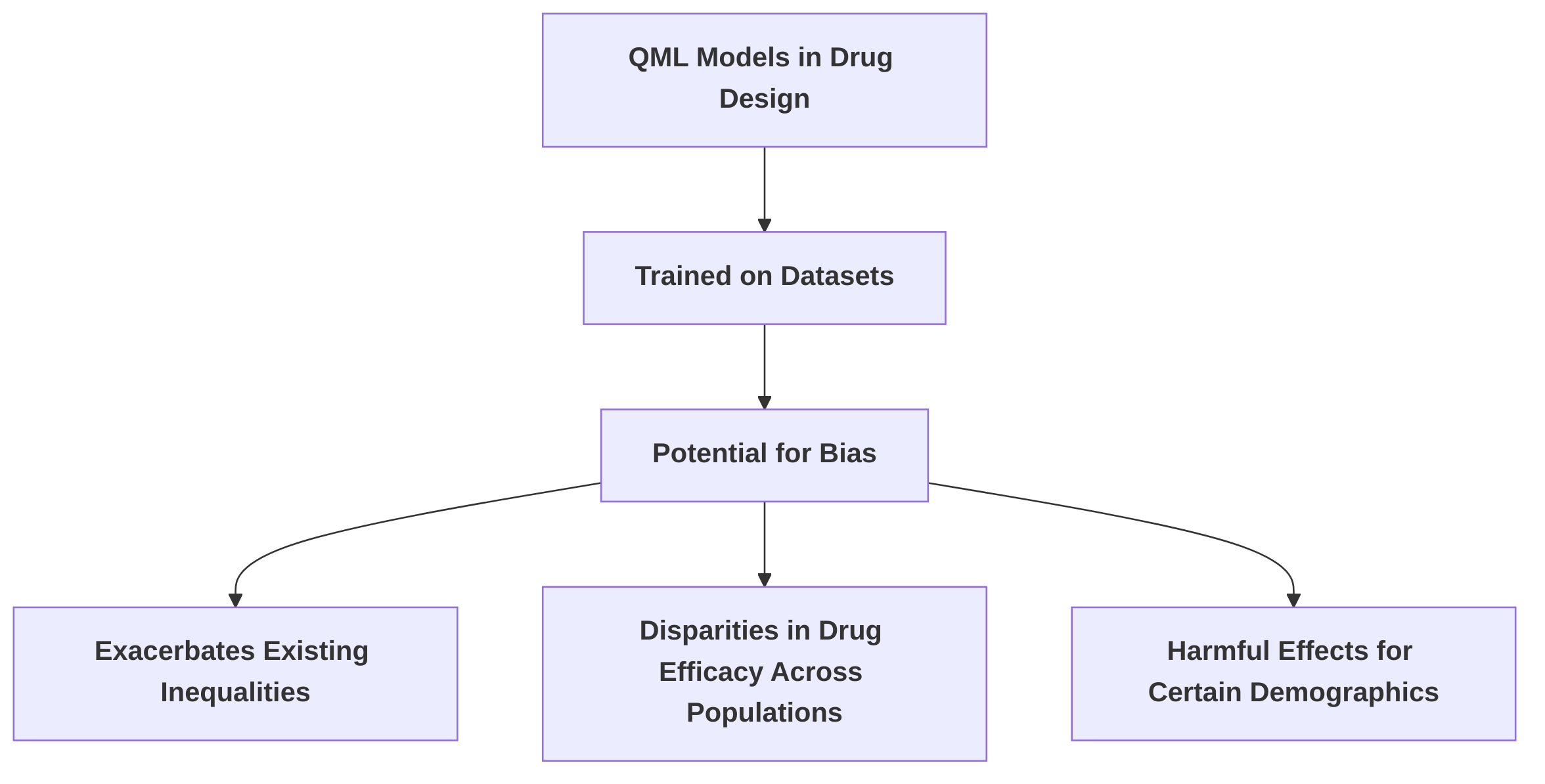
If these models are trained on biased or unrepresentative datasets, they could exacerbate existing inequalities in drug efficacy across different populations or demographic groups . For instance, a QML model trained predominantly on data from one ethnic group might develop drugs that are less effective or even harmful for others, perpetuating health disparities.

Furthermore, the integration of quantum computing with other emerging technologies like AI and blockchain, while revolutionary for drug discovery, necessitates careful consideration of ethical implications and societal impacts for responsible development and deployment . The ability of quantum computers to process vast amounts of data at unprecedented speeds raises significant privacy and security concerns, particularly when dealing with sensitive genetic and health information . Robust encryption protocols and secure data storage systems are essential to protect patient confidentiality as sensitive patient data is analyzed using quantum computers . The potential for quantum computers to decrypt encrypted data more easily in the future could pose substantial risks to patient privacy, underscoring the urgent need for robust post-quantum cryptographic solutions and regulatory frameworks that safeguard privacy while fostering innovation in the life sciences sector . In response to these concerns, techniques such as quantum federated learning are being explored as frameworks to train models collaboratively without directly sharing private data, with further privacy enhancements through differential privacy and the intrinsic randomness of quantum mechanics, naturally mitigating some data leakage issues associated with classical ML property predictors .

The accelerated drug development timelines promised by quantum computing also have profound societal impacts on healthcare systems and patient access to new treatments. While faster drug discovery is generally beneficial, it could put pressure on healthcare systems to adapt quickly to new treatment paradigms and ensure equitable access. This includes addressing challenges related to drug pricing, insurance coverage, and the infrastructure required to deliver advanced therapies globally . The potential for misuse of powerful simulation capabilities, such as designing bioweapons or highly addictive substances, also constitutes a significant ethical concern, necessitating robust oversight and international cooperation.

Researchers and developers bear a significant responsibility in ensuring the ethical and beneficial application of these technologies. This includes advocating for inclusive frameworks, promoting the democratization of access to quantum computing resources, and actively engaging in policy-making for responsible technological stewardship . Considering different stakeholder perspectives—including patients, healthcare providers, policymakers, industry leaders, and civil society organizations—is crucial for identifying potential areas of consensus or conflict in ethical frameworks. This multi-stakeholder approach can help in developing clear guidelines and regulations that ensure responsible innovation, protect vulnerable populations, and promote the equitable distribution of the benefits derived from quantum molecular simulation. The ethical dilemmas surrounding the use of quantum computing in drug design and personalized medicine necessitate proactive engagement to establish guidelines that prioritize human well-being and societal equity .

7. Future Outlook and Potential Impact

The future of quantum computing in molecular simulation and materials design is projected to be transformative, moving beyond current limitations to enable unparalleled computational capabilities . Significant advancements are anticipated in both hardware and algorithmic development, paving the way for more accurate, efficient, and industrially practical simulations .

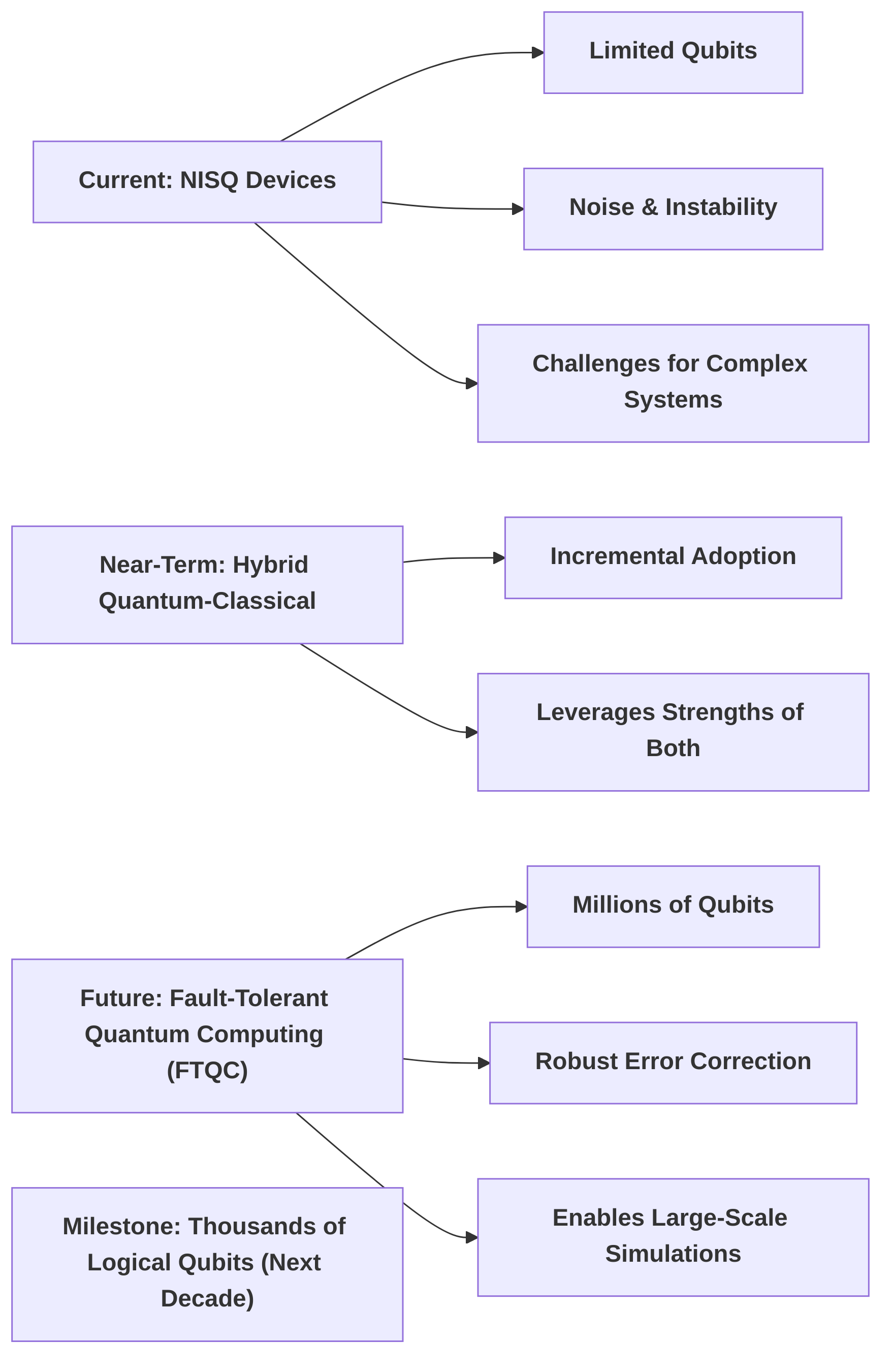
Hardware breakthroughs are critical for scaling quantum simulations. The current reliance on Noisy Intermediate-Scale Quantum (NISQ) devices often presents challenges such as qubit instability, noise, and limited qubit counts, which hinder the simulation of complex systems. The progression towards fault-tolerant quantum computing (FTQC) is a key anticipated development, with estimates suggesting this could be achieved within 10-20 years, necessitating advancements in qubit coherence, error mitigation techniques, and the development of millions of qubits for robust error correction . Near-term hybrid quantum-classical systems are expected to dominate, enabling incremental adoption and allowing for more immediate applications by leveraging the strengths of both classical and quantum computation . The next significant milestone involves processors with thousands of logical qubits, which are expected within the next decade with sustained investment, moving towards production-level workflows . Such hardware improvements, including advancements in cryogenics and control electronics, are essential to overcome existing limitations and enable the simulation of industrially relevant compounds that currently require an impractical number of qubits .

Algorithmic innovation is equally vital for enhancing the accuracy and efficiency of molecular simulations. While the Variational Quantum Eigensolver (VQE) is expected to remain a workhorse for near-term quantum simulation, scaling to larger molecules and deeper physics will necessitate improvements in fidelity and accuracy . Future research directions include the development of noise-resilient ansatzes specifically tailored for various molecular structures and the exploration of alternative quantum algorithms beyond VQE and Quantum Phase Estimation (QPE) for molecular simulation . Furthermore, the refinement of pseudopotentials and the exploration of more sophisticated hybrid quantum-classical approaches, which combine classical computational power with quantum resources, are crucial for making quantum simulations practical for real-world industrial applications . The integration of quantum computing with other emerging technologies, such as Artificial Intelligence (AI) and blockchain, is also anticipated to accelerate the discovery and development of novel therapeutic compounds .

The broader implications for fields such as drug discovery and materials science are profound. Quantum simulations are expected to significantly accelerate discovery and design processes by reducing the need for extensive trial-and-error in laboratory testing, enabling more precise molecular modeling . This transformation is particularly promising for life sciences, where quantum computing can revolutionize drug discovery and personalized medicine development through rapid simulations and complex molecular modeling . The projected economic impact on the pharmaceutical industry alone is substantial, with estimates nearing $200 billion by 2035, driven by a shift from lab-based R&D to in silico target identification and drug design, leading to significant savings and more precise therapies . This could also enable the pursuit of treatments for neglected and rare diseases, opening new market opportunities . Early applications are also envisioned in analyzing theoretical models of quantum materials like the Hubbard model, understanding multi-metal systems relevant to drug design and ammonia production, and exploring superconductivity . Potential future applications extend to photocatalytic reactions, carbon capture, solar cells, and batteries .

Connecting to the limitations discussed in previous chapters, the proposed advancements directly aim to overcome hurdles such as qubit stability, noise, and algorithmic complexity . The development of quantum-centric supercomputing (QCSC) and advanced hybrid algorithms like DMET-SQD demonstrate that current quantum computers can already aid in simulating complex molecules with chemical accuracy, setting a precedent for future medical advances and disease understanding . Progress in increasing qubit counts and mitigating noise is actively working towards more impactful simulations . Specific research directions include developing scalable quantum algorithms for medicinal chemistry, protein folding, pharmacokinetic modeling, and virtual screening, alongside the evolution of regulatory frameworks for validation and reproducibility . The long-term vision encompasses end-to-end quantum-enabled drug development, incorporating AI-assisted quantum generative design and real-time feedback loops, with cloud-based platforms democratizing access to these advanced capabilities . Understanding quantum circuit design and hybrid algorithm integration is crucial for developers contributing to this evolving field, as it transitions from theoretical concepts to applied science . Ultimately, while quantum computers are powerful tools, their full potential will only be realized through sustained collaboration between domain experts and significant experimental work .

8. Conclusion

The nascent field of quantum computing has demonstrated significant foundational progress in its application to molecular simulation and materials science, marking a pivotal shift from theoretical concepts to tangible demonstrations. Early investigations have consistently underscored the inherent advantage of quantum computers in handling complex electron interactions at the atomic level, which is a significant bottleneck for classical computational methods in accurately simulating molecules and materials . This capability is crucial for unlocking a wide array of applications, from accelerated drug development to the discovery of novel materials .

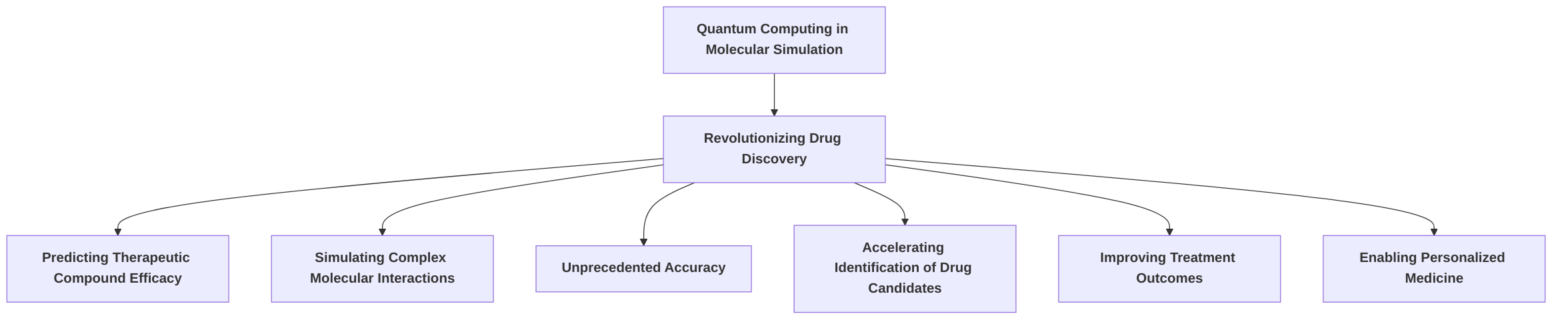
A primary focus of early applications has been in drug discovery, where quantum computing is revolutionizing the prediction of therapeutic compound efficacy through unprecedented simulations of complex molecular interactions . This has paved the way for identifying novel drug candidates and improving treatment outcomes, with profound implications for personalized medicine .

Specific, impactful early demonstrations include the successful application of the Variational Quantum Eigensolver (VQE) algorithm. For instance, VQE has been employed to compute the ground state energy of the LiH molecule using frameworks like MindSpore Quantum, yielding results comparable to the highly accurate Full Configuration Interaction (FCI) method . Furthermore, VQE implementations have shown excellent agreement with FCI benchmarks for small molecules like $H\_3^+$, $OH^-$, $HF$, and $BH\_3$, even outperforming classical unrestricted Hartree-Fock (UHF) methods . These achievements highlight VQE's evolution from theoretical toy models to meaningful simulations across chemistry, condensed matter, and physics, continuously improving in scale and fidelity even on imperfect quantum hardware .

Beyond ground state calculations, significant strides have been made in simulating larger molecular systems and complex reactions. A new approach demonstrated on IonQ systems has enabled accurate and efficient electronic structure simulation of larger molecular systems by decomposing problems into smaller subproblems, thus significantly reducing qubit requirements . This method successfully simulated a 10-hydrogen atom ring to chemical accuracy, a crucial step for materials science and chemistry . Moreover, collaborative efforts have showcased a more than 20-fold speedup in simulating key pharmaceutical reactions using hybrid quantum-classical workflows, reducing simulation times from months to days and signifying a critical advancement for the pharmaceutical industry . The successful demonstration of hybrid methods like DMET-SQD on current quantum hardware further indicates that chemical accuracy for complex molecules is achievable even without fault-tolerant systems, offering a viable path for quantum-centric scientific computing .

Despite these promising early results, the field of quantum computing in molecular simulation operates under a dual nature: immense promise tempered by substantial challenges. Current quantum hardware limitations necessitate the adoption of hybrid quantum-classical approaches . Quantum systems remain highly susceptible to noise, and scaling them to a sufficient number of reliable qubits presents significant difficulties due to specialized requirements and limited qubit counts . While advancements are needed in hardware, data loading, and algorithms, the increasing accessibility provided by quantum cloud computing platforms offers a pathway for various industries to engage with these resources .

Realizing the full potential of quantum computing requires addressing several critical challenges. These include improving hardware scalability, ensuring algorithm reliability, developing a skilled workforce, and establishing regulatory validation . While generic exponential speedups for ground state calculations are not yet definitively proven, exponential advantages may emerge for simulating time evolutions, particularly in complex, strongly correlated systems where classical methods falter . Specific niches, such as multi-metal systems and enzyme catalysis (e.g., FeMoco), are identified as key areas where quantum computers could provide significant value, impacting drug discovery and catalyst design . Furthermore, while new quantum algorithms have reduced the complexity of computing molecular energy derivatives, substantial developments are still necessary for quantum computers to effectively contribute to molecular dynamics simulations . The use of pseudopotentials in quantum simulations of materials also shows promise for more efficient resource utilization, laying groundwork for future industrial innovation, despite current hardware limitations and high resource demands for complex simulations .

The future trajectory of quantum computing in molecular simulation is poised for further advancements, driven by the ongoing synergy between quantum computing and artificial intelligence, particularly machine learning. This integration is expected to enhance efficiency in searching large datasets via generative modeling and pattern recognition, potentially reducing costs and time-to-market for new drugs . The continuous development in both Noisy Intermediate-Scale Quantum (NISQ) and fault-tolerant quantum computing promises to reduce the time and cost associated with drug development, ultimately benefiting public health . Quantum computing is positioned to complement and eventually redefine conventional drug discovery paradigms, enabling faster, more accurate development of novel therapeutics and fostering a deeper understanding of molecular complexity . The significant investments from both public and private sectors underscore the widely recognized potential of quantum computing to revolutionize industries reliant on complex data analysis, including drug design, quantum chemistry, and biomolecular simulations, offering profound benefits for scientific research and healthcare innovation . These early applications, therefore, represent foundational steps towards realizing the full potential of quantum computing in scientific discovery, paving the way for a future where intractable problems become solvable and scientific breakthroughs are accelerated.

References

Study Suggests Today's Quantum Computers Could Aid Molecular Simulation https://thequantuminsider.com/2025/07/15/study-suggests-todays-quantum-computers-could-aid-molecular-simulation/

Quantum-machine-assisted Drug Discovery: Survey and Perspective - arXiv https://arxiv.org/html/2408.13479v2

How quantum computing is transforming drug discovery - Fractal Analytics https://fractal.ai/article/quantum-computing-in-life-sciences

How does quantum computing work in solving real-world problems in drug discovery? https://milvus.io/ai-quick-reference/how-does-quantum-computing-work-in-solving-realworld-problems-in-drug-discovery

Molecular Electronic Structure Calculation via a Quantum Computer - arXiv https://arxiv.org/html/2303.09911v4

Modelling molecules: How quantum computers simulate at the atomic level - Riverlane https://www.riverlane.com/blog/modelling-molecules-how-quantum-computers-simulate-at-the-atomic-level

Efficient Quantum Computation of Molecular Forces and Other Energy Gradients https://research.google/pubs/efficient-quantum-computation-of-molecular-forces-and-other-energy-gradients/

A New Approach for Accurately Simulating Larger Molecules on IonQ Computers https://ionq.com/resources/new-approach-for-accurately-simulating-larger-molecules

5 Exciting Quantum Computing Applications (with Examples) - BlueQubit https://www.bluequbit.io/quantum-computing-applications

Applications in chemistry and material science | Introduction to Quantum Computing for Business https://introtoquantum.org/applications/chemistry/

Quantum Computing Applications: A Technological Revolution - blog.colobridge.net https://blog.colobridge.net/en/2025/05/applications-of-quantum-computing-en/

IonQ Speeds Quantum-Accelerated Drug Development Application in Partnership With AstraZeneca, AWS And NVIDIA https://thequantuminsider.com/2025/06/09/ionq-speeds-quantum-accelerated-drug-development-application-in-partnership-with-astrazeneca-aws-and-nvidia/

The convergence of quantum computing and early drug discovery - Kvantify https://www.kvantify.com/inspiration/the-convergence-of-quantum-computing-and-early-drug-discovery

Quantum Computing Method May Make Simulating Materials More Practical https://thequantuminsider.com/2024/12/21/quantum-computing-method-may-make-simulating-materials-more-practical/

Quantum Computing Applications: Drug Discovery https://quantumzeitgeist.com/quantum-computing-applications-drug-discovery/

Variational Quantum Eigensolver (VQE) Breakthroughs https://postquantum.com/quantum-computing/variational-quantum-eigensolver-vqe/

Applications of Quantum Computing in Drug Design and Molecular Simulation - YMER https://ymerdigital.com/uploads/YMER240731.pdf

VQE Application in Quantum Chemistry Computing - MindSpore https://www.mindspore.cn/mindquantum/docs/en/r0.6/vqe\_for\_quantum\_chemistry.html